What is KL?
KL stands for "knowledge language", and is a new domain specific programming language for interactive fiction developed at Strand.
Broadly speaking, KL can be split into the "K" part and the "L" part; with the "L" part a general purpose programming language, and the "K" part, specific features for manipulating knowledge structures and the representation of general purpose knowledge.
It was understood from the start that any domain specific language that does not also support general programming is too limited. Which is why we need both "K" and "L".
But why do we need a new language at all?
This is a good question. First let me point out that almost all established interactive fiction systems have their own IF language, and this goes to the root of IF. For example, Zork was written in ZIL - Zork Implementation Language.
Pushing the boundaries of IF and solving new problems means new solutions, and those solutions could enormously benefit from a new-generation implementation. That's why languages like KL are needed - to solve today's problems.
This first part, will be covering the general purpose features of KL (ie "L") and part two will be tackling "K".
KL Basics
KL is a minimalist programming language with a homoiconic, Lisp-like syntax and features drawn from scheme and others along with new ideas, but is semantically different in many ways. KL is designed with efficiency in mind and removes a lot of overhead often present in Lisp like languages;
-
KL does not generate garbage when evaluating. Data within KL are reference counted and dereferenced objects are destroyed immediately.
-
KL supports destructive operations on data.
-
KL does not use, so called, cons lists to build its lists. Consequently the familiar
carandcdrare meaningless; although(car x)can be implemented(at x 0).
Lists in KL are the basic building blocks of all data structures, but they are not "cons" pairs as in traditional lisp/scheme implementations. Instead, internally, Lists are chunks of contiguous memory chained together, each containing several elements. In this way, short lists occupy one block of memory, while long lists consist of multiple segments. Inserting into, or deleting from, a long list will only resize one segment. Regardless of the internal structure, Lists appear as one logical object within KL. Indexing into a KL List is therefore a lot more efficient than having to walk a traditional cons list.
In memory, lists look a bit like this:

The base KL data types are:
- Int
- Number (float)
- String
- List
- Set
- Symbol
- Function/Macro
Although details to be explained further on, let's give the flavour by writing some traditional examples;
Here's the usual recursive factorial;
(setq factorial
(fn (x)
(ife (= x 0) 1
(* x (factorial (- x 1))))
))Or, if you want, iteratively;
(setq ifactorial
(fn (x)
(local
(setq f 1)
(for i 2 (+ x 1) (setq f (* f i)))
f
)
))Interestingly, in the above setq, local and for are actually macros not primitives. It's very easy to build KL in KL.
Instead of going into the usual (boring) language detail, we're going to focus on four main important KL differences to traditional systems.
KL1: Destructive Operations
Many list operations work destructively, in other words, they modify the underlying list data, and since objects are reference counted in KL, any and all references will see a changed list.
For example, let's try to make cons, the Lisp function that constructs a new list from an element and an existing list;
(setq cons (fn (a l) (insert l a 0)))OK, so it's not really the same because here the insert method destructively modifies its given list so that we insert an element a at position 0 in list l. But in most cases this does the same job.
> (setq a (list 'bar))
(bar)
> (cons 'foo a)
(foo bar)
> a
(foo bar)a is now bound to (foo bar) and not just (bar) as before.
Although much of modern fashion is for immutable data, the ability to modify data such as lists and sets in place is most important for KL. This will become especially relevant later for the discussion of world state and knowledge representation. The whole "world" is a set, and updating it will require in-place modification.
KL2: Sets
Sets work a lot like lists, except they are unordered and cannot have repeats. The purpose of sets is to organise arbitrary large data efficiently, for both modification and retrieval.
In KL, a set is denoted by braces {} rather than parentheses.
Internally, sets are actually lists. If you imagine ensuring the content of lists is ordered and put lists inside other lists, you can imagine the internal structure of the KL set.
Consequently, you get a multi-way tree;
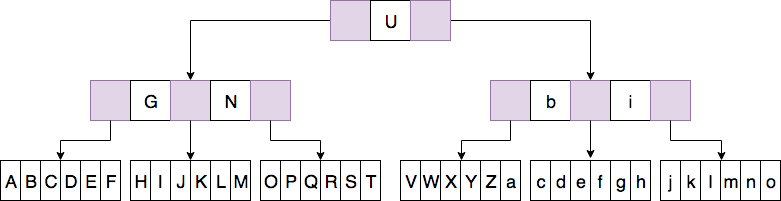
Lists and sets both start life as a single "list" node of a few contiguous entries. This means a set of a few and a list of a few are the same cost in memory. Later, we'll see one problem of representing information is that you have no idea in advance of which small lists will expand to large lists. A list of fish perhaps? All is well, until you're building a fish-keeping database!
Let's look at an example;
Here is a randomised sequence of numbers 0 to 99 that we add to a Set:
31 55 67 3 12 5 91 62 37 60 16 79 78 87 64 90 8 33 45 52 4 9 22 23 98 95 72 15 54 36 38 71 26 44 34 30 25 7 94 39 63 69 19 1 48 10 93 49 13 68 51 76 0 32 99 84 56 59 58 77 11 61 75 17 29 92 66 2 27 47 81 83 53 6 40 21 70 41 97 43 80 50 82 73 65 74 86 42 88 18 46 20 24 35 96 85 57 14 89 28Resulting in the following Set:
{0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 5 6 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99}But shown as a list, we see the internal morphological structure:
(((0 1 2 3) 4 (5 6 7 8) 9 (10 11 12 13 14)) 15 ((16 17 18 19 20 21 22) 23 (24 25 26 27 28 29 30) 31 (32 33 34 35 36)) 37 ((38 39 40 41) 42 (43 44 45 46) 47 (48 49 50 51 52 53) 54 (55 56 57 58 59) 60 (61 62 63 64 65 66)) 67 ((68 69 70 71 72 73 74 75) 76 (77 78 79 80) 81 (82 83 84 85 86) 87 (88 89 90 91 92 93) 94 (95 96 97 98 99)))Note: In practice, the list segment sizes in the set are much bigger than 4-8 elements shown here for illustration (eg ~1024).
Anytime, you insert of retrieve from a set, KL uses the tree layout to efficiently perform the operation.
KL3: Reify the environment
If lists can be efficient trees, then why not use a tree for symbol binding environments and then let the programmer modify it destructively!
In KL, the current environment may be affected by the env primitive.
(env)Returns the current environment, and
(env expr)Sets the current environment.
Earlier on i mentioned that local is not a primitive. local is a definition that extends the current binding environment so that locally set symbols act like local variables (eg in ifactorial above).
With env we can build local;
(setq local
(def args
(
(env (list (tree) (env)))
(eval args)
(env (at (env) 1))
)
))Here, local takes all its args as a list, but first it extends the current environment with an empty (tree). Then it evaluates its arguments within this new environment. Finally, it restores the original environment.
NB: def provides lazy evaluation of args. Use of fn instead of def would strictly evaluate args too early.
Turns out, although this works, it's a bit clunky and a more elegant solution is to allow the eval primitive to take an optional environment. Using this approach we get a tidier definition of local;
(setq local
(def args
(eval args (list (tree) (env)))))Now as total binding environment hackers, we can leverage the same thing in reverse to build a properties store.
(setq cat {(location mat) (name "tibbles") (likes fish)})
(setq fish {(location bowl)})
(setq getprop
(fn (p s)
(eval 'p (eval s))
))Let's try it out;
> (getprop 'name cat)
"tibbles"
> (getprop 'location cat)
mat
> (getprop 'location (getprop 'likes cat))
bowlProperty lookup is just eval in disguise!!
Later, we'll build on this principle to make much more sophisticated information stores.
KL4: Function "closures" are also Lists
That's right, in KL there are no closures in the usual sense - functions are just lists!
By now, you've realised that in KL we're running with scissors!
Let's see what factorial defined earlier really is;
> factorial
<< (ife (= _1 0) 1 (* _1 (factorial (- _1 1)))) >>The << and >> indicators are just for show, but it's actually a list.
The traditional function closure holds a binding environment which it uses for both local variables and for parameters. This is useful, but what if we don't have any?
Why have the baggage of extending the binding environment for each and every closure invocation, when do don't always need it.
In KL, we give this to the programmer. Above we saw local as a way to extend the current binding environment when it's needed. That's how we do it in KL - only when needed.
Parameters also suck because if we put them into a local binding environment like a closure, we both have to put them in and look them up when referenced.
In KL, functions are much simpler and one of the reasons why KL is so fast. The body of the function definition gets turned into a simple list but parameter references are translated into indexes; _1, _2 etc which index into a temporary array of parameters held by the caller.
So;
- In the function body, parameter references become indexes at parse time.
- Those indexes vector into a contiguous array.
- no binding environment is needed.
- no special data structure is needed to represent a function.
- temporary local variables can be made by manually creating an environment
- not creating an environment just means those symbols are bound in the parent environment, which may well be harmless.
Consequently, for many functions, calling them is just a "GOSUB". That's why a lot of KL is actually in KL. Consider;
(setq first (fn (l) (at l 0)))
(setq inc (def (v) (setq v (+ 1 v))))
(setq for
;; eg (for x 1 10 (print x)) NB: 10 not included
(def (v a b e)
(forall 'v a
(while (< v b) e (inc v)))
))KL's low overhead for simple function calls encourages functionality to be factored out making the program more generic without compromise.
In compiled languages, it's the compiler that does the heavy lifting here by inlining small functions. KL is designed to be an interpreted language, but without serious drawbacks.
Conclusion
This overview is only a very brief introduction and does not even begin to cover the more advanced features, such as the knowledge operators. Nor have we really shown the application of KL to interactive fiction.
In the sequel; "Part 2: "K", We'll cover the knowledge operators |- and ~ as well as their empowered counterparts, |= and ~~, and show how we can begin to build and query structured knowledge.
Hopefully after that, we'll have covered enough to start explaining the application to IF in Brahman in the developing KL/IF/Brahman system.
